Měření kolem nás (31) Můstky – 2
18. 8. 2021 | Orbit Merret, spol. s r. o | www.orbit.merret.cz
Můstků je velké množství a je možné, že právě v tuto chvíli vzniká další. Stále však platí, že můstky slouží pro usnadnění nebo pro umožnění měření některých elektrických veličin. A to je místo pro můstky
Můstků je velké množství a je možné, že právě v tuto chvíli vzniká další. Stále však platí, že můstky slouží pro usnadnění nebo pro umožnění měření některých elektrických veličin. A to je místo pro můstky.
Thomsonův můstek
Chceme-li ve čtyřbodovém zapojení měřit velmi malý odpor můstkovou metodou, musíme použít dvojitý (Thomsonův) můstek. Místo přímého měření napětí na měřeném rezistoru se toto napětí porovnává s napětím na odporovém normálu, kterým protéká stejný proud jako měřeným rezistorem.
Celý můstkový obvod se skládá ze dvou částí. Rezistory P, p, Q, q jsou součástí komerčně vyráběného můstku. Na schématu jsou tyto obvody zakresleny uvnitř čárkovaně vyznačeného obdélníku.
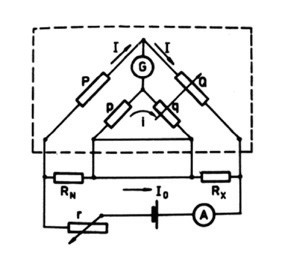
Obr. 1. Thomsonův můstek
Je-li můstek vyrovnán, je mezi body, ve kterých je připojen indikátor G, nulový rozdíl potenciálů. Rezistory p, q pak teče stejný proud i. Napětí na rezistoru P musí být rovno napětí na rezistorech RN a p.
Můstek je určen pro měření odporů menších než 1 Ω. Přesné měření vyžaduje čtyřbodové zapojení měřeného rezistoru RX rezistorového normálu RN. Jsou-li rezistory RN a RX menší než 1 Ω lze dosáhnout toho, že rezistory P, p, Q, q budou alespoň tisíckrát větší než RN či RX, což znamená, že proudy i a I budou nejméně tisíckrát menší než I0. Spád napětí na přívodních vodičích k můstku a na svorkách neovlivní proto podstatněji výsledek měření.
Na přesnost měření Thomsonovým můstkem má vliv odchylka způsobená necitlivostí, případně dodatečné chyby vyplývající z přetížení proudových rezistorů, zkoušeného a srovnávacího, ze změn teploty a výskytu dodatečných elektromotorických sil v systému. Vzhledem k závadám a omezením tradičních technických můstků, dochází v současné době k tendenci konstruovat elektronické měřicí přístroje k měření malých odporů v rozsahu od jednotlivých mikroohmů do několika set ohmů. Přístroje umožňují měřit velmi malé odpory s rozlišením až 0,1 µΩ. Důležitou vlastností moderních mikroohmmetrů je jednoduchost ovládání, použití různých měřicích režimů a možnost spolupráce s počítačem.
De Sautyho můstek
De Sautyho můstek se používá k měření kapacity.Můstek je tvořen dvěma rezistory, dvěma kondenzátory a nulovým indikátorem. Aby bylo možno můstek úplně vyvážit, musely by být kondenzátory Cx (měřený kondenzátor) a CN (vyvažovací kondenzátor) bezeztrátové. To však v praxi neplatí, což znamená, že nelze můstek úplně vyvážit. Tato metoda se dá využít pro měření kapacity kondenzátorů s malým ztrátovým činitelem, stačí-li vyvážení na minimální výchylku. Nehodí se pro měření kondenzátorů s pevným dielektrikem.
Kompenzaci nedokonalostí kondenzátorů navrhl Grover. Neznámý kondenzátor C1 s vnitřním odporem r1 představujícím ztráty ve větvi ab se porovná se standardním známým kondenzátorem C2 spolu s jeho vnitřním odporem r2 na rameni ad. Rezistory R1 a R2 jsou zapojeny externě v sérii s C1 a C2. Můstek může být vyvážen změnou některého z neindukčních rezistorů R3 nebo R4.
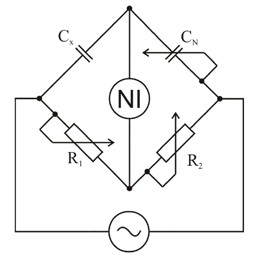
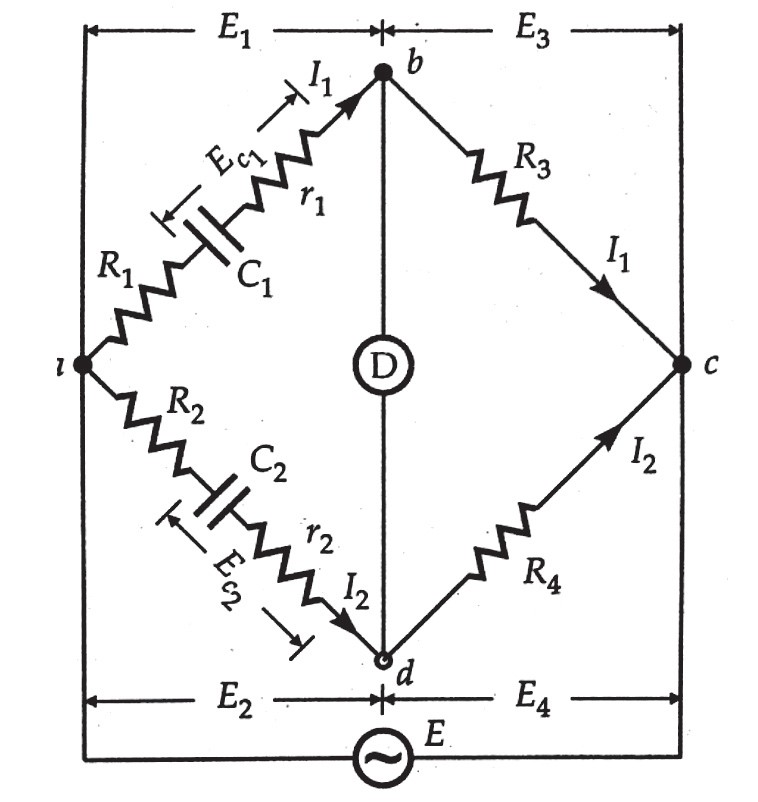
Obr. 2. De Sautyho můstek, Obr. 3. Kompenzace nedokonalostí kondenzátorů navržená Groverem
Scheringův můstek
Poprvé můstek užil německý fyzik Harald Schering v roce 1920.Scheringův můstek se používá k měření kapacit (úpravou i pro velké kapacity až desítky mF), ztrátového činitele (přesnost až 0,01 %) a permitivity izolantů. Přesnost měření kapacit bývá řádově 0,1 %. Frekvence zdroje bývá 15 až 1 000 Hz.
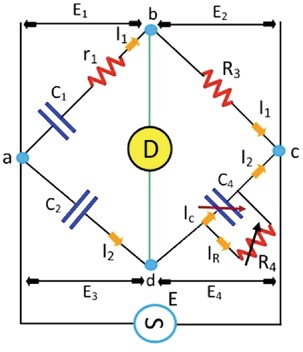 Obr. 4. Scheringův můstek
Obr. 4. Scheringův můstek
C1 – kondenzátor, jehož kapacita má být stanovena
r1 – sériový rezistor představující ztrátu kondenzátoru C1
C2 – standardní kondenzátor (termín standardní kondenzátor znamená, že není ztrátový)
R3 – neindukční rezistor
C4 – proměnný kondenzátor
R4 – proměnný neindukční rezistor paralelní s proměnným kondenzátorem C4
Careyho – Fosterův můstek
Carey-Foster můstek se používá k měření nízkého odporu nebo k porovnání dvou téměř stejných rezistorů. Princip fungování můstku je podobný Wheatstonovu můstku.
Nechť P, Q, R a S jsou čtyři rezistory použité v můstku. Rezistory P a Q jsou známé, zatímco R a S jsou neznámé rezistory. Drát délky L je umístěn mezi rezistorem R a S. Rezistory P a Q jsou nastaveny tak, aby poměr P / Q byl ekvivalentní R / S. Poměr odporu je ekvivalentní posunu kontaktu na posuvném vedení drátu.
Při měření se zjišťuje pozice jezdce na drátu kdy je můstek vyvážený, tedy délka l1 a poté délka l2 při výměně rezistorů R a S mezi sebou. Lze také samozřejmě zjišťovat odpor pouze R (při známém odporu S). Rozdíl mezi odpory R a S je stejný jako rozdíl odporu drátu mezi pozicemi (vzdálenostmi) l1 a l2.
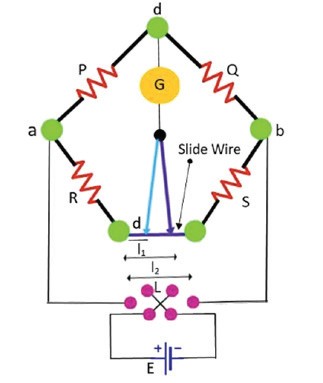
Obr. 5. Careyho – Fosterův můstek
Wienův můstek
Tento můstek navrhl Max Wien v roce 1891. Používá se k měření kapacity a také k měření frekvence vstupního napětí.Pomocí tohoto můstku lze měřit frekvence od 100 Hz do 100 kHz. Přesnost můstků je mezi 0,1 - 0,5 %. Můstek se používá pro různé další aplikace, jako je měření kapacity, v analýze harmonického zkreslení a ve vysokofrekvenčních oscilátorech.
Tento můstek je frekvenčně citlivý. Je tedy obtížné najít rovnovážný bod. Vstupní napájecí napětí obvykle není čistě sinusové a harmonické v napájecím napětí narušují rovnovážný stav můstku. K překonání tohoto problému se v můstku používá filtr. Filtr se zapojuje do série s nulovým detektorem.
Rezistory R1 a R2 jsou mechanicky propojeny a mají vždy stejný odpor. Rovnováhy je tedy dosaženo při určité frekvenci a určitém poměru R4 a R3 . Při znalosti C1 R1 C2 a R2 lze snadno vypočítat frekvenci vstupního napětí.
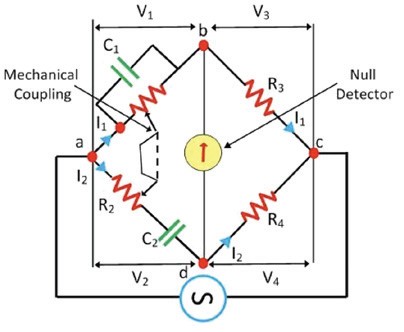
Obr. 6. Wienův můstek
Heavisideův můstek
Tento můstek vytvořil Oliver Heaviside. Zajímavé je, že jeho strýcem nebyl nikdo jiný, než Ch. Wheatstone, který Heavisideovu rodinu finančně podporoval.Můstek slouží k měření vzájemné indukčnosti cívek.
Obvod tohoto můstku se skládá ze čtyř neindukčních rezistorů r1, r2, r3 a r4 připojených k ramenům 1-2, 2-3, 3-4 a 4-1. V sérii k tomuto můstku připojena měřená cívka. Na svorky 1 a 3 je přivedeno napětí. V rovnovážném stavu můstku mezi body 2–4 elektrický proud neprotéká, takže pokles napětí na 2–3 se rovná poklesu napětí na 4–3. Vyrovnáním úbytků napětí 2-4 a 4-3 a dosazením hodnot do rovnic je pak možné vypočítat hodnotu vzájemné indukčnosti.
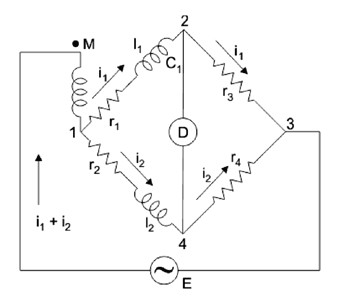
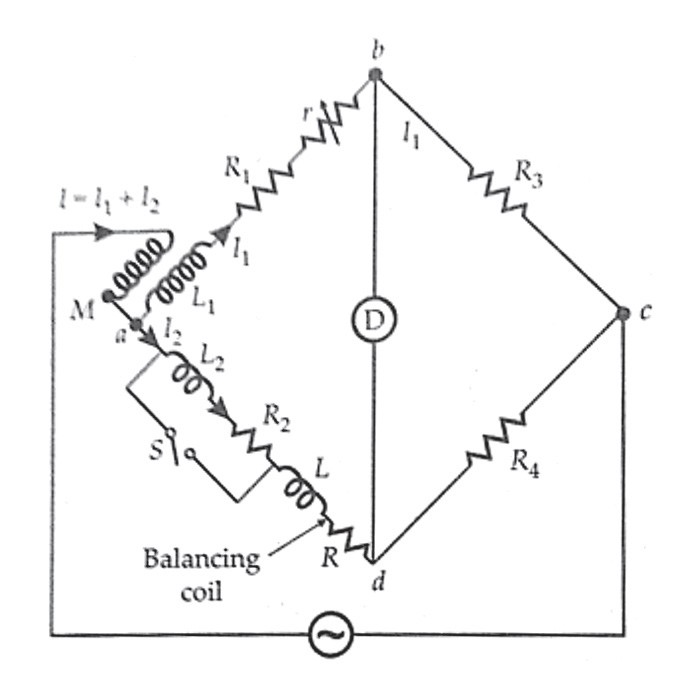
Obr. 7. Heavisideův můstek, Obr. 8. Campbellův můstek
Campbellův můstek
Používá se k měření vlastní indukčnosti. Můstek je modifikací Heavisideova můstku. V tomto případě je do ramene a-d v sérii s testovaným induktorem zahrnuta další vyrovnávací cívka R. Do ramene a-b je vložen další rezistor r. Vyvážení se získá změnou M a r. R3 a R4 jsou shodné.
Zkratový spínač je umístěn přes měřenou cívku R2, L2. Měření se provádí dvakrát, s otevřeným spínačem a druhá se zavřeným spínačem. Hodnoty jsou pak dosazeny do rovnic, umožňující výpočet vlastní indukčnosti cívky M.
(Pokračování)
Zdroje:
Wikipedia
https://cs.wikipedia.org/wiki/Scheringův_můstek
https://circuitglobe.com/schering-bridge.html
https://www.industrial-electronics.com/measurement-testing-com/eemi_6.html
http://home.zcu.cz/~formanek/VYUKA/Data1/MT/mt-prednasky/K02mustek.pdf
https://www.spslan.cz/images/PDF1314/rekvalifikace/mustek.pdf
https://www.eeeguide.com/wagner-earth-connection/




