Záhada analemmy – historický základ využívania slnečného svetla
| Záhada analemmy – historický základ využívania slnečného svetla Richard Kittler a Stanislav Darula, Keď nám profesor Karel Hannauer roku 1949 v prvom ročníku architektúry a pozemného staviteľstva na bratislavskej technike vysvetľoval v predmete základy architektonickej tvorby, ako sa ľahko graficky určujú dráhy Slnka, netušili sme, o aký starý a podstatný ľudský poznatok ide. Zrejme to nevedel ani prednášateľ, ani jeho učiteľ profesor Vojtech Krch z pražskej ČVUT, ktorý vo svojej uznávanej knihe [1] na strane 42 píše, že „diagram slunečních stínů je nejznámější konstrukcí k určení stínu svislice. Pravděpodobně ho prvně použili Cooper a Julian v r. 1919. Představuje vlastně stíny vrcholu tyče vztyčené v bodě pozorování na vodorovnou rovinu.„ Ako sa len mýlil! Pre spomínanú vertikálnu tyčku mali už v starom Grécku termín „gnómon„ a bola základom slnečných hodín. Vitruvius [2], rímsky teoretik architektúry, popísal v roku 13 pred Kr. ich konštrukciu, ktorú nazval „analemma„, a priznal, že tieto znalosti boli už vtedy veľmi staré, pravdepodobne z chaldejskej, t. j. novobabylonskej éry okolo roku 600 pred Kr. Pravdepodobnejšie však je, že prvý takýto geometrický náčrtok pochádzal z sumerskej ríše, keďže na hlinených tabuľkách z roku 1500 pred Kr. sa zachoval pôdorysný plán mesta Nippur [3, s. 200], a ešte prv okolo roku 2780 pred Kr. [4, s.17] tu existovala tzv. sexagonálna sústava čísiel s delením roka na 360 dní, mesiaca na 30 dní, dňa na 24, resp.12 hodín i delenie kruhu na 360°. Okrem toho iný údaj [4, s.27] hovorí, že okolo roku 2020 pred Kr. sa v Mezopotámii používali slnečné hodiny a v Egypte obelisk ako gnómon. 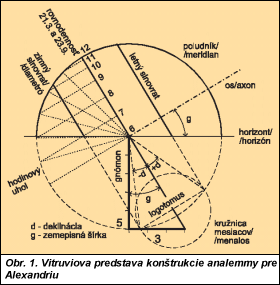 Ten, kto chce pri zostrojovaní slnečných dráh sledovať český preklad Vitruvia [2, s. 310], presne neporozumie výkladu analemmy, pretože na náčrtku a v texte sú pomýlené označenia záchytných bodov. Anglický preklad [5, s.271] je presnejší a tým zrozumiteľný a dá sa dnešku priblížiť aj vysvetlením v [6]. Pretože vo Vitruviovej dobe nebolo možné spoliehať sa na zemepisnú šírku miesta, používal sa gnómon s predpísaným pomerom výšky k dĺžke jeho tieňa v čase rovnodennosti (21. 3. a 23. 9.) v danej lokalite na určenie základnej dráhy Slnka v týchto dňoch. Pre Káhiru alebo Alexandriu to bol pomer 5 : 3 (čiže arctg 3/5 = 30,96° pri presnej zemepisnej šírke Káhiry 30,1° a Alexandrie 30,6°). Podobne by sa dnes mohli zvoliť pomery pre Prahu napr. 5 : 6 (t. j. arctg 6/5 = 50,96° pre zemepisnú šírku 50°), popr. pre Bratislavu by mohol byť približný pomer 8 : 9 (t. j. arctg 9/8 = 48,36° pre zemepisnú šírku 48,17°). Ak uvážime, že termín „analemma„ čiže náčrtok [7, s.183] použili Diodoros Alexandrijský aj neskôr Klaudios Ptolemaios ako názov publikácie, je možné predpokladať, že išlo o tradovaný nákres deskriptívnej geometrie s konštrukciou slnečných dráh v ortogonálnom priemete na vertikálnu rovinu s orientáciou sever-juh. Súčasne to bol návod na riešenie veľmi praktickej úlohy kalendára a časomiery v podobe slnečných hodín. Návod Vitruvia sa dá stručne vysvetliť podľa obr. 1. Keď poznáme pomer výšky gnómonu a jeho tieňa v čase rovnodennosti alebo zemepisnú šírku miesta, na fiktívnej oblohe (polguli či hemisfére) sa zdanlivá dráha Slnka 21. 3. javí v priemete ako priamka s vrcholom na obvode meridiánu alebo poludníkového kruhu s postavením Slnka o dvanástej hodine pravého slnečného času. Pretože každý deň sa Zem otočí okolo svojej osi raz za 24 hodín, t. j. o 360°/24 = 15° za hodinu, na sklopenej kružnici celodennej dráhy možno nájsť polohu Slnka v každej hodine. Samozrejme, aj v ročnom cykle sa kruhové dráhy postupne premiestňujú v rámci deklinácie (maximálneho naklonenia zemskej osi o ±23,45°, popr. podľa Vitruvia o 360°/15 = 24°). Tak je možné na tzv. kruhu mesiacov (tzv. menaeus nad rovnobežkou so zemskou osou, ktorá sa volá logotomus) určiť umiestnenie dráhy v ľubovolnom dátume počas celého roka. 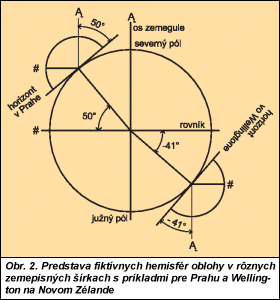 Dnes si už vieme predstaviť, že v určitej lokalite na zemeguli (napr. v Prahe alebo na druhej strane na Novom Zélande vo Wellingtone, obr. 2) je rovina dráhy Slnka v dni rovnodennosti vždy rovnobežná s rovinou rovníka a os každodennej zemskej rotácie je zrejme rovnobežná s osou zemegule. Netreba zabudnúť, že v ľubovolnom mieste na zemeguli je horizontálna rovina, t. j. horizont tangentou so sklonom kolmým k zemepisnej šírke. Rozvojom trigonometrie a astronómie v Alexandrii, najmä pričinením Ptolemaia, sa doriešili aj niektoré nedôslednosti konštrukcie analemmy. Ptolemaios objasnil priemety oblohovej hemisféry do troch vzájomne kolmých rovín, takže okrem poludníka dostal pôdorysné eliptické priemety slnečných dráh a tým sa dalo určiť presné postavenie Slnka pomocou jeho uhlovej výšky, resp. zenitnej vzdialenosti a azimutálneho odklonu od juhu v ľubovolnom čase a na hociktorom mieste na Zemi [7, s.183]. Okolo roku 150 po Kr. sa dali zostrojiť ortografické diagramy slnečných dráh, ako boli pre Bratislavu už dávnejšie publikované v [8, s.18] a [9, s.48–51]. Štúdiom vzťahov uhlových rozovretí v rovine a na guli sa Ptolemaiovi asi podarilo určiť zmeny východu a západu Slnka podľa závislosti: cos (15° Hvs) = tg g tg d, resp. kde H je číslo hodiny v pravom slnečnom čase, t. j. H = 0 až 24, resp. Hvs je hodina východu Slnka, g geografická šírka lokality, d deklinácia Slnka v danom dni roka. 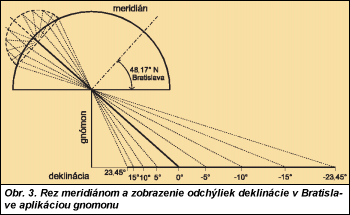 V dnešnom tvare sa však tento vzorec mohol písať až neskôr, keď rannorenezančný duch viedol k objavovaniu starovekých poznatkov. Ten pobádal v roku 1461 do Ríma nemeckého matematika a astronóma Johana Müllera, ktorého neskôr nazvali Regiomontanus. Tu študoval a prekladal Ptolemaiov Almagest, novoskoncipoval trigonometriu ako samostatnú matematickú disciplínu [10, s. 12] a vo svojej knihe o trojuholníkoch zaviedol označovanie funkcie tangens [4, s. 96]. Neskôr v rokoch 1467 až 1471 bol jedným z prvých profesorov na bratislavskej Akadémii Istropolitane, takže až vtedy sa asi mohol začal písať horeuvedený vzorec v súčasnej podobe. Z podmienky pre východ Slnka, keď uhlová výška Slnka nad horizontom hs je nulová, t. j. sin hs = 0, resp. jeho zenitná vzdialenosť zs je 90° a cos zs = 0, sa dal odvodiť obecný vzťah pre výšku Slnka, pretože cos g cos d cos (15° H) = sin g sin d čo je dnes už tradovaný základný vzorec pre výpočet výšky Slnka v ľubovolnom čase a lokalite [11]. Súbežne so zdokonaľovaním matematických a astronomických poznatkov sa technicky riešilo meranie času. Od slnečných a presýpacích, popr. vodných hodín sa postúpilo k mechanickým, napred so závažím (vynález kňaza Pacificusa z Verony okolo roku 850), až k vreckovým s naťahovacím perom (od norimberského zámočníka P. Henleina z roku 1505). Ich pravidelný chod sa stále spresňoval podobne ako aj merania pravého slnečného času na poludňajšom meridiáne. Známa je Ulug-begova hvezdáreň v Samarkande z roku 1420 so 40metrovým gnómonom, tzv. meridiánové oká alebo drážky s otvormi orientovanými presne na juh a pod.
Namiesto fiktívnej oblohovej hemisféry si teraz treba predstaviť reálnu polguľovú kupolu s meridiánovou drážkou presne v smere juhu s gnómonovým vrcholom v stredovom bode gule. Takáto drážka dovoľuje osvetliť podlahu len prúžkom slnečných lúčov o dvanástej hodine pravého slnečného času, pričom gnómonový vrchol tieňa označí uhol deklinácie (na obr. 3 pre Bratislavu, t. j. pre 48,17° severnej zemepisnej šírky). Podľa tieňa gnómonu sa letná stupnica plusovej deklinácie zužuje a presúva vľavo, kým zimný tieň sa predlžuje s mínusovou deklináciou na pravej strane v obr. 3. Pre určitú deklináciu sa zapisovala podľa hodiniek časová odchýlka a tak sa zistil a upresňoval viacminutový rozdiel medzi pravým slnečným a absolútne pravidelným hodinkovým časom. V každom prípade sa pôvodný názov analemma už v staroveku používal ako termín pre deskriptívny náčrtok s ortografickým priemetom slnečných dráh na vertikálnu rovinu poludníka (t. j. v smere sever-juh), pre návrh slnečných hodín s tieňom gnómonu na horizontálnu rovinu. Je zrejmé, že oveľa neskôr sa pôvodný význam strácal s upresňovaním merania času mechanickými hodinkami a v prenesenom význame sa použil pre názov krivky, ktorá definuje závislosť medzi pravým slnečným a hodinkovým časom v ročnom cykle. Takúto súvislosť propaguje aj súčasná americká Spoločnosť analemma (http://www.analemma.org). Spätný pohľad do minulosti nás stále presviedča o obrovskom potenciáli poznatkov o javoch v prírode, ktorý mali naši predkovia. Bez možností výpočtovej techniky len trpezlivou a systematickou prácou s primitívnymi prostriedkami dospeli k záverom, ktoré často znovu objavujeme. Zanechali nám vzácny odkaz a nemalo by sa zabúdať, že spoliehanie sa na rozum a ľudskú múdrosť je efektívnejšie ako zdanlivo dokonalé automatizovanie myšlienkových pochodov. Ukazuje sa, že každý pohľad do minulosti je obohatením budúcnosti. Poďakovanie [1] KRCH, V.: Oslunění budov a vnitřků. Techn. vědecké vyd., Praha, 1952. [2] VITRUVIUS, M. P.: Deset knih o architektuře. (Český preklad A. Otoupalík). Vyd. Svoboda, Praha, 1979. [3] ZAMAROVSKÝ, V.: Na počiatku bol Sumer. Mladé letá, Bratislava, 1984. [4] PATURI, F. R.: Kronika techniky. Fortuna Print, Bratislava. 1993. [5] VITRUVIUS, M. P.: The ten books on architecture. (Anglický preklad M. H. Morgan). Dover Publ. Inc., New York, 1914 a 1960. [6] KITTLER, R. – DARULA, S.: Analemma the ancient sketch of fictitious sunpath geometry or Sun, time and history of mathematics. Architectural Science Review, 2004 (v tlači). [7] KOLMAN, A.: Dějiny matematiky v starověku. Akademie, Praha, 1968. [8] KITTLER, R.: Slnko a svetlo v architektúre. SVTL, Bratislava, 1956. [9] KITTLER, R. – MIKLER, J.: Základy využívania slnečného žiarenia. Vyd. VEDA, Bratislava, 1986. [10] ŠALÁT, T. a kol.: Malá encyklopédia matematiky. Obzor, Bratislava, 1978. [11] VINNACIA, G.: Il corso del sole in urbanistica ed edilizia. Ed. U. Hoepli, Milano, 1939. [12] HYKŠ, P. – HRAŠKA, J.: Slnečné žiarenie a budovy. Vyd. Alfa, Bratislava, 1990. | ||||||||||||||||||||||




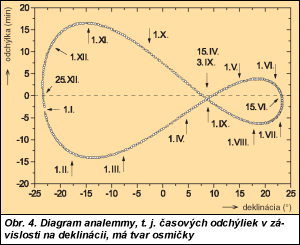 Pritom sa tento počas roka menil, no zhodný bol v štyroch dňoch, a to 3. septembra, 25. decembra a 15. apríla a 15. júna. V súčasnosti sa súvislosť slnečného a hodinkového času vyjadruje viacerými tzv. časovými rovnicami [9, s. 37], ktorých premennou najčastejšie býva číslo dňa v roku podobne ako pri definovaní deklinácie [9, s. 27]. Pôvodne sa dávali tieto časové rozdiely do súvisu hlavne s deklináciou a zistilo sa, že graf s údajmi deklinácie na osi x a časovými rozdielmi na osi y vytvára krivku v tvare ležatej osmy (na obr. 4), popr. pri prevrátení súradníc v tvare 8 [12, s. 7]. Táto krivka sa tiež už dávnejšie nazývala analemmou, niekedy analemna či analemnata, a tak tento termín dostal dvojzmyselný význam.
Pritom sa tento počas roka menil, no zhodný bol v štyroch dňoch, a to 3. septembra, 25. decembra a 15. apríla a 15. júna. V súčasnosti sa súvislosť slnečného a hodinkového času vyjadruje viacerými tzv. časovými rovnicami [9, s. 37], ktorých premennou najčastejšie býva číslo dňa v roku podobne ako pri definovaní deklinácie [9, s. 27]. Pôvodne sa dávali tieto časové rozdiely do súvisu hlavne s deklináciou a zistilo sa, že graf s údajmi deklinácie na osi x a časovými rozdielmi na osi y vytvára krivku v tvare ležatej osmy (na obr. 4), popr. pri prevrátení súradníc v tvare 8 [12, s. 7]. Táto krivka sa tiež už dávnejšie nazývala analemmou, niekedy analemna či analemnata, a tak tento termín dostal dvojzmyselný význam.