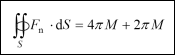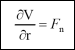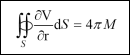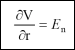| Vývoj názorů na podstatu elektřiny (62) Vliv teorie potenciálu
Teorie potenciálu měla vliv i daleko mimo svůj obor a stala se vzorem četným jiným oborům matematické fyziky. Gauss rovněž zformuloval definici množství elektřiny. Odvodil ji z Coulombova zákona. Podle ní jednotkou elektřiny je takové množství elektřiny, které ve vakuu odpuzuje stejné množství elektřiny vzdálené 1 cm silou 1 dynu. Gauss v této souvislosti dospěl i k významnému teorému, který byl důležitý pro další rozvoj teorie elektřiny. Dodnes je v učebnicích označován jako Gaussův zákon či Gaussova věta. V originálu měl tvar: 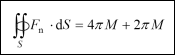 kde M je souhrn hmot nacházejících se uvnitř určitého objemu, M’ souhrn hmot spojitě rozložených na povrchu, dS prvek povrchu ohraničujícího objem, Fn síla, kterou volně rozložené hmoty působí na prvek dS v kolmém směru. Jak bylo později dokázáno, lze tento vztah získat z Greenovy věty. Nejsou-li hmoty rozloženy na povrchu, lze sílu vyjádřit potenciální funkcí: 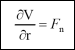 kde r je vzdálenost bodu na normále k povrchu. Pak lze napsat: 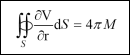
a místo hmoty M je uvažován elektrický náboj Q či součet elektrických nábojů. 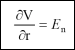 Pro vakuum měl Gaussův zákon v tehdy uvažovaných jednotkách tvar: 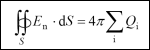 Z Gaussova zákona vyplývají pro teorii elektřiny tyto důležité závěry: silokřivky začínají na kladných nábojích a končí na záporných nábojích, je-li algebraický součet kladných a záporných nábojů uvnitř uzavřené plochy nulový, je celkový tok intenzity elektrického pole plochou rovněž nulový, nejsou-li uvnitř uzavřené plochy žádné náboje a počet vstupujících a vystupujících siločar od vnějších nábojů je stejný, celkový tok intenzity elektrického pole plochou je nulový. Gaussův zákon je platný pro jakékoliv rozložení elektrického náboje uvnitř libovolné uzavřené plochy. Je obecnější než Coulombův zákon, protože ten platí pouze pro elektrické pole vytvořené statickými elektrickými náboji. Gaussův zákon platí i pro elektrické pole vytvořené změnou magnetického pole. Oba zákony lze jeden z druhého odvodit. Pro magnetismus Gaussův zákon v určité modifikaci rovněž platí. Při respektování charakteru uzavřenosti magnetických siločar je zřejmé, že magnetický tok určený levou stranou rovnice musí být vždy nulový. Gaussův přínos teorii elektřiny a magnetismu měl zásadní a trvalý význam. Jeho práce dovršila výstavbu teoretických základů elektřiny a magnetismu založených na koncepci okamžitého silového působení na dálku. Gaussova nechuť k hypotézám jej zastavila před problémy elektrodynamiky. Svou roli sehrál i jeho věk. Fyzikou se totiž začal zabývat ve svých 54 letech a téměř desetiletá „titánská“ činnost ve zcela nové oblasti vyčerpala jeho síly. Započaté dílo však předal povolanému žákovi. 10.8 Wilhelm Eduard Weber Mladý vědec
Na rozdíl od Gausse Wilhelm Eduard Weber (obr. 1) žil již od útlého dětství v akademickém prostředí a v úzkém kontaktu se vzdělanými lidmi různého zaměření. Byl pátým dítětem profesora teologie na univerzitě ve Wittenbergu. Dva z jeho bratrů působili jako profesoři anatomie a fyziologie na univerzitě v Lipsku, nejstarší bratr se stal ministrem.  Obr. 1. Wilhelm Eduard Weber
* 24. 10. 1804 Wittenberg (nyní Německo)
† 23. 6. 1891 Göttingen (Německo) Zájem tří bratrů o vědu bezpochyby vzbudil rodinný přítel, profesor medicíny a přírodovědy Christian August Langguth, v jehož domě Weberovi žili. Dalším nájemníkem zde byl i proslulý fyzik Ernst Florence Friedrich Chladni (1756–1827). Od roku 1813 žila rodina Weberova v Halle. Univerzita v Halle byla v roce 1817 oficiálně spojena s univerzitou ve Wittenbergu. Zde již ve velmi mladém věku začal Wilhelm vědecky spolupracovat se svým bratrem Ernstem Heinrichem, téměř o deset let starším, na problematice vodního vlnění. Experimentální zkoumání v roce 1825 vyústilo ve vědeckou publikaci, která uvedla Wilhelmovo jméno ve známost ve vědeckých kruzích. V průběhu studia na univerzitě v Halle byl mladý Weber nejvíce ovlivňován fyzikem Johannem Salomo Christophem Schweiggerem (1779–1857) a pravděpodobně i matematikem Johannem Friedrichem Pfafem (1765–1825). Svou doktorskou disertační práci, věnovanou akustické vazbě jazýčku a vzduchové dutiny varhanní píšťaly, vypracoval roku 1826 u Schweiggera, o rok později se habilitoval dalším propracováním téže problematiky na lektora a krátce nato byl jmenován pomocným profesorem na univerzitě v Halle. Svou přednáškou na berlínském zasedání Společnosti německých přírodovědců a lékařů v září 1828, věnovanou varhanním píšťalám, vzbudil Gaussovu pozornost. Gauss ve Weberovi rozpoznal cenného spolupracovníka, zainteresoval ho na své práci o geomagnetismu a získal pro něho i místo profesora v Göttingenu. Zde pak Weber strávil spoluprací a v blízkém přátelství s Gaussem šest plodných a pro Webera bezpochyby i přínosných let. Podrobněji bylo o tomto období pojednáno v odstavci věnovaném C. F. Gaussovi. (pokračování) |