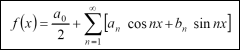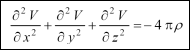Vývoj názorů na podstatu elektřiny (58)

Vývoj názorů na podstatu elektřiny (58)

Ing. Josef Heřman, CSc.

Další životní osudy J. B. J. Fouriera
Zdrojem dalších životních Fourierových peripetijí byl jeho vztah k Napoleonovi. Rozhodnutím Mongeho, tehdy též ministra námořnictví, se zúčastnil Napoleonova tažení do Egypta, během nějž Napoleon rozpoznal jeho velmi dobré administrativní schopnosti. Po návratu do Francie Fouriera jmenoval prefektem departmentu s centrem v Grenoblu a udělil mu titul barona. Definitivní pád Napoleona roku 1815 pro Fouriera znamenal další potíže v osobním životě (žil určitou dobu jen z malé penze) i komplikace ve vědeckém životě, pramenící z jeho nízké politické reputace (problémy při jeho volbě do Akademie apod.).

Fourierova řada
Zájem o problematiku šíření tepla byl u Fouriera vzbuzen již za jeho pobytu v Egyptě, avšak základní práci vytvořil v době svého působení v Grenoblu. Svůj rozsáhlý memoár věnovaný šíření tepla, vycházející z řešení difuzní rovnice, zaslal v roce 1807 Akademii. Uvedl zde i vyjádření funkce f(x) řadou, jež byla po něm později pojmenována Fourierova řada: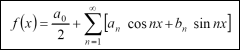

kde a₀, a_n, b_n jsou koeficienty, pro které Fourier odvodil příslušné vztahy.

Členové komise, která práci posuzovala, Laplace, Monge i matematik Sylvestre Francois Lacroix (1765–1843), byli nakloněni práci přijmout, avšak Lagrange byl ostře proti. Souviselo to s jeho řešením vibrace struny z roku 1750. Fourierova práce v podobě tohoto memoáru nebyla nikdy publikována.

V této souvislosti pro úplnost dodejme, že problém vyjádření „libovolné“ funkce trigonometrickými řadami byl v polovině 18. století právě při řešení vibrace struny předmětem diskuse mezi L. Eulerem a D. Bernoullim (1700–1782, švýcarský matematik, fyzik a lékař; zabýval se teorií pravděpodobnosti, přibližným řešením algebraických rovnic pomocí rekurentních řad), který použil k řešení trigonometrické řady a byl přesvědčen, že jde o obecné řešení. Vzniklé pochybnosti o přípustnosti tohoto řešení odstranil až Fourier. Nicméně v roce 1807 to byla myšlenka zcela nová a tak průkopnická, že u Lagrangeho vyvolala odpor. Ke správnému pochopení Fourierovy metody významně přispěl německý matematik Peter Gustav Lejeune Dirichlet (1805–1859), jenž jako první podal přesný důkaz konvergence Fourierových řad.

Makroskopický přístup
Fourier pokračoval v Laplaceových prioritách řešení fyzikálních problémů matematickou analýzou, avšak rozdílným způsobem, který byl i rozhodným posunem od Laplaceovy fyziky sil. Fourier na rozdíl od Laplaceových i Poissonových mikroskopických modelů přešel svou teorií tepla k makroskopickému (fenomenologickému) popisu jevů, tedy nepřihlížel k vlastní fyzikální podstatě jevu. Teplo pokládal za kontinuální tok, přičemž jeho množství prošlé jednotkovou plochou za jednotku času je úměrné rozdílu teplot – vycházel tedy z makroskopických veličin. Jeho metoda umožnila v matematické analýze vycházet i z empirických zákonů.

Fourier i Poisson se hluboce zajímali o využití matematiky ve fyzice a oba svými pracemi významně přispěli i k objevům v „čisté“ matematice. Fourier v předmluvě k svému základnímu dílu, Analytické teorii tepla, k tomu napsal: „Důkladné zkoumání přírody je nejčastější příčinou matematických objevů. Toto zkoumání dává bádání určitý cíl a má tu výhodu, že vylučuje nejasné otázky a výpočty, které nevedou k cíli...„.

Obr. 1. Siméon Denis Poisson
* 21. 6. 1781 Pithiviers (Francie); † 25. 4. 1840 Seeaux (Francie)

10.5 Siméon Denis Poisson

Střet s Fourierem
Posledním velkým teoretickým mechanikem francouzské školy byl Siméon Denis Poisson (obr. 1). Patřil do skupiny významných matematiků, kteří byli spjati s počátky pařížské Ecole Polytechnique. Úzce spolupracoval s Laplaceem a jím ovlivňován se zabýval mnoha fyzikálními problémy. Měl velký talent převádět je do matematické formy. To se však někdy projevilo v tom, že matematicky zpracovával i jevy touto formou již vysvětlené. Bylo tomu tak i po publikování Poissonova náčrtu teorie tepla v roce 1815; to vyvolalo ostrou kritiku Josepha Fouriera. V úvodu své kritiky Fourier napsal: „Poisson má velký talent využít ho na práci jiných. Použít ho k objevení toho, co již je známé...„. Poisson oprávněnost Fourierovy kritiky uznal a akceptoval ji. Nicméně na vztazích mezi oběma vědci se to příliš neprojevilo. Avšak je třeba objektivně uvést, že svými díly Traité de mécanique (Traktát o mechanice – vydán v roce 1811), Nouvelle théorie de l‘action capillaire (Nová teorie kapilarity – roku 1831) a Théorie mathématique de la chaleur (Matematická teorie tepla – roku 1835) uvedl tyto obory na vyšší úroveň.

Poissonova rovnice
Pro teorii elektřiny a magnetismu je důležitý Poissonův příspěvek k matematickému zpracování působení přitažlivé síly v teorii gravitace. Zájem o tuto problematiku vzbudila práce britského matematika a fyzika Jamese Ivoryho (1765–1842) v letech 1812 až 1813. Zdrojem Poissonova zkoumání byl Laplaceův integrál funkce V a Laplaceova rovnice, která, jak bylo již uvedeno, platí pro přitahování v místech, kde není hmotnost. Dokázal, že pro body nacházející se uvnitř přitahující hmoty, tedy v místech, kde je přítomna hmota, má uvažovaná rovnice tvar: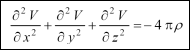

kde r je hustota látky objemového prvku.

Tato rovnice vešla do fyziky jako Poissonova rovnice, a Laplaceova rovnice je tudíž jejím jednodušším případem. Pro úplnost dodejme, že Poisson kromě této rovnice stanovil i rovnici pro body nacházející se na povrchu. Ta však vyvolávala pochyby a Carl Friedrich Gauss (1777–1855) vyzval v roce 1839 k ověření této rovnice důkazem.

Poisson byl první, kdo se pokusil využít matematický aparát, který se osvědčil v analytické mechanice pro teorii elektřiny a magnetismu, konkrétně pro elektrostatiku. Vycházel z prací Roberta Symmera (1700–1763), Henryho Cavendishe (1731–1810), Charlese Augustina Coulomba (1736–1806) a dalších.

(pokračování)