Vývoj názorů na podstatu elektřiny (57)

Vývoj názorů na podstatu elektřiny (57)

10.3 Pierre Simon Marquis de Laplace

Cesta k vědě
Pierre Simon Marquis de Laplace (obr. 1) byl posledním z vůdčích matematiků 18. století. Pocházel z rodiny malého statkáře v Normandii. Již při studiu na střední škole vzbudil pozornost svým velkým matematickým nadáním. Na doporučení d’Alemberta¹⁾ se stal profesorem matematiky na pařížské vojenské škole. Zde byl jeho posluchačem i Napoleon Bonaparte. Pozvolna ve své kariéře stoupal, zastával mnoho pedagogických i administrativních funkcí. Během revoluce se mimo jiné podílel i na výstavbě známé pařížské Ecole Polytechnique. Do historie matematiky a fyziky se Laplace zapsal především položením základů některých matematických disciplín, např. teorie pravděpodobnosti, teorie parciálních diferenciálních rovnic a teorie potenciálu, zvlášť významné pro teoretickou fyziku.

Teorie potenciálu
Teorii potenciálu uvedl Laplace i ve svém proslulém pětisvazkovém díle Mécanique céleste (Nebeská mechanika) z let 1799 až 1825. Matematicky v něm formuloval a vyřešil problém stability drah jednotlivých planet a zveřejnil první teorii vzniku sluneční soustavy.

Obr. 1. Pierre Simon Marquis de Laplace
* 28. 3. 1749 Beaumnot-en-Ange (Francie) † 5. 3. 1827 Paříž (Francie)

O tomto díle existuje mnoho anekdot. Dobře je např. známa odpověď, kterou měl Laplace říci Napoleonovi na jeho poznámku, že o Bohu se Laplace ve své knize vůbec nezmiňuje. „Pane, nepotřeboval jsem tuto hypotézu,„ údajně odpověděl autor díla. O úrovni Laplaceova matematického myšlení svědčí výrok překladatele čtyř Laplaceových knih do angličtiny: „Kdykoliv jsem narazil na Laplaceův obrat což snadno vyplyne, byl jsem si jist, že mám před sebou hodiny tvrdé práce, abych vyplnil mezery a nalezl a dokázal, jak nám to snadno vyplyne.„

Newton odvodil závěr, že sílu, kterou homogenní koule přitahuje hmotný bod, je možné vyjádřit vztahem pro vzájemné přitahování hmotných bodů. Vyvstal problém přechodu od hmotných bodů k objemovému rozdělení hmoty libovolného tvaru. V osmdesátých letech 18. století hledal Joseph Louis Lagrange způsob vyčíslení síly, kterou těleso libovolného tvaru přitahuje libovolně umístěný hmotný bod. Dokázal, že síla, kterou je přitahován hmotný bod soustavou hmotných bodů, je možné rozložit na součet parciálních derivací určité funkce. Pro soustavu sil působících podle inverzního kvadratického zákona mezi bodem M a soustavou hmotných bodů mi je tato funkce v každém bodu prostoru o průvodiči r_i definována sumou: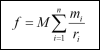

J. L. Lagrange tuto funkci nijak nepojmenoval. Laplace z tohoto závěru vyšel a roku 1782 ve své publikaci Teorie gravitace dokázal, že pro kompaktní hmotu o hustotě r (hmotnost na jednotku objemu) lze Lagrangeovu funkci, kterou označil V, vyjádřit ve tvaru: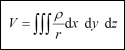

kde r je délka průvodiče určujícího polohu místa.

Tato funkce pro místa, kde není rozložena žádná hmotnost, vyhovuje rovnici: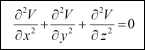

Rovnice byla zavedena do fyziky jako Laplaceova rovnice. Zde je třeba uvést, že k této rovnici v roce 1752 došel i Leonhard Euler při odvozování hlavních rovnic hydrodynamiky. Funkce V byla později označena jako potenciální funkce.

Obr. 2. Jean Baptiste Joseph Fourier
* 21. 3. 1768 Auxerre (Francie) † 16. 5. 1830 Paříž (Francie)

Problém nalezení síly v kterémkoliv bodě prostoru se tak redukoval na problém řešení parciální diferenciální rovnice pro daný případ (při daných okrajových podmínkách). Po většinu 19. století byla matematická teorie sil věnována obecným metodám řešení a zobecnění Laplaceovy rovnice. Vlastní teorií elektromagnetismu se ale Laplace zabýval jen okrajově. Připomeňme jeho spolupráci na Biotově a Savartově zákonu (viz ELEKTRO 10/2003).

10.4 Jean Baptiste Joseph Fourier

Teorie šíření tepla
Joseph Fourier (obr. 2) se elektřinou a magnetismem přímo nezabýval. Přesto jeho přínos a význam pro teorii elektřiny a magnetismu jsou velké a přesáhly staletí. Fourierova teorie šíření tepla, kterému věnoval své základní dílo Théorie analytique de la chaleur (Analytická teorie tepla), vydané v roce 1822, přinesla matematické metody, které patří ke klasickým nástrojům teoretické fyziky. Platí to především o vyjádření libovolných funkcí (které ale splňují určité podmínky) řadami nebo integrály harmonických funkcí. V teorii kteréhokoliv procesu vlnění – zvuku, povrchového vlnění na kapalinách, elektromagnetických kmitů apod. – má Fourierovo rozložení v čistě harmonické kmity důležitý a zásadní význam. Fourierova matematická teorie tepla se stala základem pro George Simona Ohma (1789–1854) při odvození základního zákona vedení elektrického proudu (viz ELEKTRO 7/2004).

Životní zvraty
Fourierovy životní osudy byly silně poznamenány velkými společenskými změnami a bouřlivými událostmi ve Francii na konci 18. století. Po vypuknutí Velké francouzské revoluce v roce 1789 se Fourier vrátil ze studií v Paříži do rodného Auxerre, kde se stal místně prominentní osobností. Jeho odvaha bránit oběti teroru vedla v roce 1794 k jeho uvěznění. Osobní odvolání k Robespierovi²⁾ nebylo nic platné – byl propuštěn až po jeho popravě.

(pokračování)

¹⁾ Jean Baptiste le Rond d’Alembert, * 17. 11. 1717, † 29. 10. 1783, francouzský matematik, fyzik, osvícenský filozof. Do roku 1759 spoluvydavatel Encyklopedie, autor Úvodu k Encyklopedii, ve kterém načrtl dějiny vzniku a vývoje poznání a klasifikaci věd. Zabýval se mechanikou (zejména její matematizací), diferenciálním počtem, pohybem nebeských těles a teorií gravitace.

²⁾ Maxmilán Robespiere byl jako buržoazní demokrat představitelem jakobínů ve Francouzské revoluci, která začala 14. července 1789 útokem na státní vězení Bastilu a jeho dobytím. V červnu 1793 byl Robespiere v čele státní moci – Národního konventu. V červenci 1794 byl se svými druhy zatčen a o několik dní později byl popraven.