Repetitorium Víte, že Pythagoras opisoval? prof. Václav Černý Poučka, že součet ploch čtverců nad odvěsnami pravoúhlého trojúhelníka je roven ploše čtverce nad jeho přeponou, byla známa již dávno před narozením Krista. Lze se o tom přesvědčit nahlédnutím do díla Šalvasútra. Šalvasútra (Pravidla provazce) shrnuje nejstarší známé poznatky posvátných nábožensko-filozofických véd („véda“ v sanskrtu znamená vědomost) z oboru geometrických konstrukcí a matematiky. Tyto knihy pocházejí ze sedmého až pátého století před Kristem, podle jiných pramenů dokonce z patnáctého až dvanáctého století před Kristem. Podstatnou část knihy Šalvasútra tvoří pravidla pro určování rozměrů náboženských kultovních staveb, které vždy musely mít strany, plochy a objemy v určitých poměrech, např. 1 : 2 : 3. Pro vytyčování staveb se používaly provazce a tyče, pro konstrukci pravého úhlu pravoúhlé trojúhelníky s celočíselnými rozměry stran (např.: 3, 4, 5; 5, 12, 13; 8, 15, 17; 7, 24, 25; 12, 35, 37 atd.). 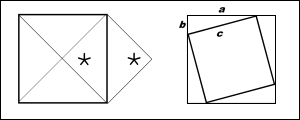
V této knize je uveden i příklad, ze kterého je zřejmé, že poučka, která je připisována Pythagorovi (572 až 507 před Kristem), byla známa již o hodně dříve: Vytyč čtverec dvojnásobného obsahu původního čtverce! Je to čtverec nad diagonálou, označené trojúhelníky jsou zřejmě shodné! Ostatně tuto poučku znali již asi dva tisíce let před Kristem v Mezopotámii a pravděpodobně i v Číně a Indii. Krásný obecný geometricko-algebraický důkaz je doložen v komentáři Číňana Čao-Ťun-Čchena (druhé nebo třetí století) ke starému traktátu „Čou-Pi“ c2 = (a + b)2 – 4(ab)/2
c2 = a2 + 2ab + b2 – 2ab
c2 = a2 + b2 | 



