Počítačová simulace, vizualizace a analýza fyzikálních polí v praxi (2. část)
Ing. Jan Růžička
konzultant v oblasti projektování
V tomto díle bude prezentovaná aplikace programu na průmyslové zařízení, elektromechanický aktuátor (EMA). Kromě magnetických parametrů pole budou analyzovány zejména silové poměry na táhlu.
V popisovaném případě bude analyzován jednoduchý model lineárního EMA (válcového elektromagnetu), zobrazeného v osovém řezu na obr. 1, který je převzat z uživatelské příručky k programu QuickField. Tam je uveden pod názvem Magn2.
Skládá se z těchto částí:
- táhlo,
- plášť,
- budicí cívka.
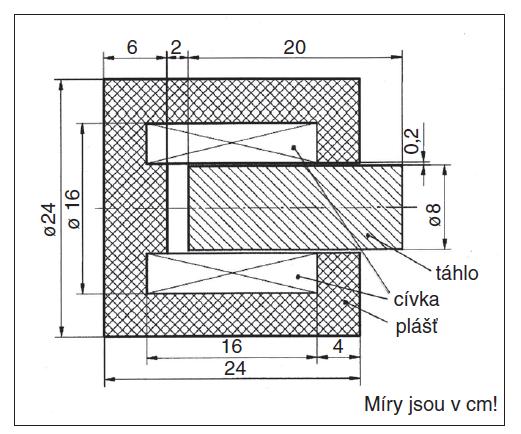
Obr. 1. Aktuátor
Příklad č. 2 – Elektromagnet
Zadání
V měděném vinutí cívky válcového elektromagnetu teče stejnosměrný proud o hustotě j = 1·106 A·m–2. Táhlo i plášť jsou zhotoveny z oceli s vlastnostmi dané křivkou B – H podle tabulky.
Úloha
- zobrazit průběh magnetické indukce v elektromagnetu,
- určit sílu působící na táhlo,
- stanovit statickou charakteristiku pro rozsah zdvihu 2 < zr < 3 cm.
Řešení
1. Příprava úlohy (preprocessing)
Po zadání jména úlohy Magn2 se vybere z nabídky standardních oblastí magnetostatika.
V dalším kroku se zvolí jako souřadný systém osová symetrie a jako délková jednotka cm.
1.1 Tvorba geometrického modelu
Jako hranice řešené oblasti se zvolí válec o délce 40 cm a poloměru 16 cm. Tak blízkou hranici k magnetu zde lze volit proto, že plášť magnetu působí jako stínění magnetického pole. Proto ve výsledku nedojde k většímu zkreslení. Bloky zde tvoří: táhlo, plášť, cívka a vzduch. K vytvoření kresby stačí pouze nástroje úsečka a obdélník. Geometrický model po zasíťování je na obr. 2.
1.2 Vlastnosti bloků
Bloky se pojmenují a zadají se fyzikální vlastnosti:
- táhlo – v zadávacím okně oblasti se zaškrtne volba nelinear a zadají hodnoty z tabulky,
- plášť – v zadávacím okně oblasti se zaškrtne volba nelinear a zadají hodnoty z tabulky,
- cívka – zde se zadá relativní permeabilita μx = μy = 1 a hustota proudu j = 1·106 A·m–2,
- vzduch – zadá se pouze μx = μy = 1.
1.3 Vlastnosti hranice
Z nabízených možností se zvolí podél celé hranice řešené oblasti podmínka nulového magnetického toku (tzv. Dirichletova podmínka).
1.4 Síť
Příprava úlohy se ukončí vygenerováním sítě. Zvolí se ve všech blocích.
2. Řešení úlohy (processing)
Proběhne z cela automaticky po kliknutí na ikonu.
| B (T) | 0,80 | 0,95 | 1,00 | 1,10 | 1,25 | 1,40 | 1,55 |
| H (A.m-1) | 460 | 640 | 720 | 890 | 1 280 | 1 900 | 3 400 |
Tabelovaná křivka
3. Analýza výsledků (postprocessing)
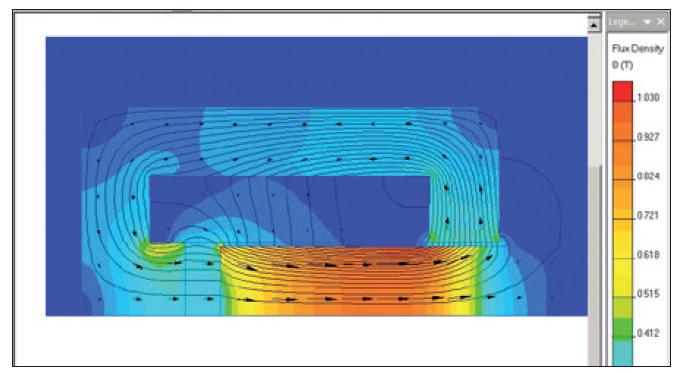
Po skončení řešení se objeví informační okno s textem: Úloha je vyřešena. Chcete zobrazit výsledky? Po volbě Ano se v řešené oblasti zobrazí ekvičáry, v popisovaném případě křivky konstantního magnetického toku Φ (Wb). Z kontextové nabídky: Vlastnosti obrázku obrázku pole se vybere: Vektory indukce B a barevná mapa indukce. Výsledek je na obr. 3. V rámci této nabídky lze upravit i hustotu ekvičar zadáním vlastní hodnoty do okénka Scale. 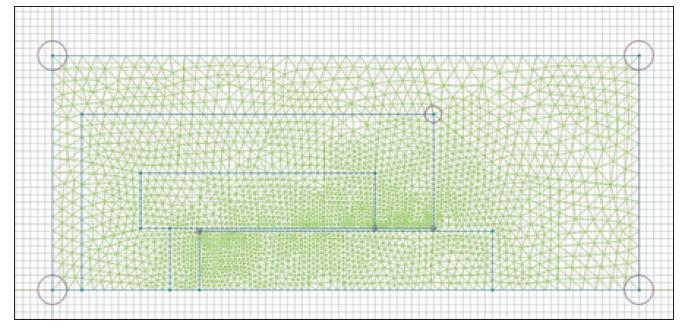
Obr. 2. Geometrický model
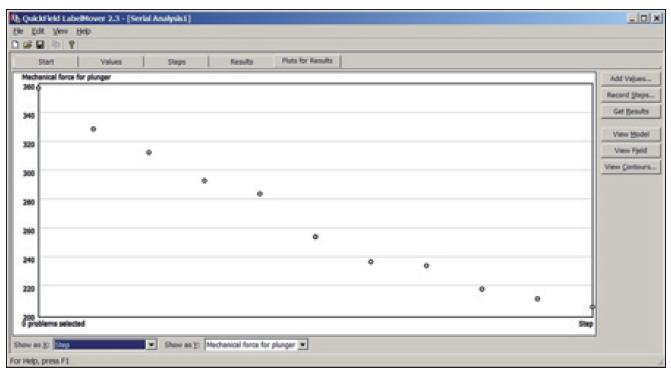
Obr. 4. Statická charakteristika
Obr. 3. Pole válcového elektromagnetu
Pro určení síly v táhlu se vybere v kresbě blok táhlo. Potom lze přejít do režimu integrálních výpočtů – Integral Calculator. V podokně se odečte: Mechanical force f = 356,82 N. To je hledaná síla působící v ose táhla. Zbývá stanovit statickou charakteristiku. Jde o závislost osové síly v táhlu na jeho poloze v plášti pro konstantní proud. Uvedená hodnota představuje její první bod. Charakteristiku je třeba vygenerovat pro dalších deset poloh táhla s krokem 0,1 cm. Nechce-li uživatel postupovat pracně ručně tak, že model opakovaně překreslí pro novou polohu a spustí výpočet, lze použít velmi užitečný nástroj programu Label Mover, který tuto činnost značně usnadní a urychlí. Zde se zadá pouze krok změny polohy, tj. 0,1 cm, a počet opakování výpočtu. Label Mover po startu pro každou polohu model automaticky překreslí a provede výpočet. Výsledek opakovaného (sériového) výpočtu je k dispozici v tabelární i grafické podobě. Výstup je na obr. 4. Tím je úloha splněna. V Label Moveru lze zadat krok změny polohy i v podobě zvoleného procenta výchozí hodnoty. Jednotlivé počítané polohy, na rozdíl od již uvedené aritmetické řady, tvoří geometrickou řadu. Při analýzách obvodů se střídavými proudy se Label Mover používá např. k rychlému generování frekvenčních charakteristik, kde se zadá krok frekvence.
Literatura:
[1 RŮŽIČKA, J.: Simulace, vizualizace a analýza fyzikálních polí v počítači. Elektro, 8-9/2011.
[2] RŮŽIČKA, J.: Počítačová simulace, vizualizace a analýza fyzikálních polí v praxi (1. část).
Elektro, 10/2011.
[3] http://www.quickfield.cz
[4] http://www.quickfield.com
[5] MAYER, D. – ULRYCH, B.: Elektromagnetické aktuátory. BEN – technická literatura, 2008.
[6] CLAYCOMB, J. R.: Applied Electromagnetics Using QuickField and MATLAB. Infinity Science Press LLC, 2008 (tuto knihu lze zakoupit na adrese [3]).
(pokračování)



